The New Improved Asymptotic
Safety FAQs
Q: What is asymptotic safety?
A: It's a way in which a quantum field theory
could be well defined at all energies without being
perturbatively renormalizable. A quantum field theory is
said to be asymptotically safe if it corresponds to a
trajectory of the renormalization group that ends at a
fixed point in the UV.
Q: Why is a fixed point good for the
theory?
A: In quantum field theory, observable
quantities such as decay rates and cross sections can be
expressed as functions of the couplings. Generically, if
the couplings are finite, also the observable quantities
will be finite. So a way of ensuring that our
description of the world has a good ultraviolet limit is
to require that it lies on a renormalization group
trajectory for which all couplings remain finite when
the energy goes to infinity. The simplest way of
achieving this is to demand that the trajectory flows
towards a fixed point. More complicated situations such
as limit cycles are also possible.
Q: So, if gravity was asymptotically
safe,
A: No. The couplings of familiar theories
such as the standard model are dimensionless and for
them the definition of a fixed point is completely
straightforward. For dimensionful couplings the
definition of a fixed point is a bit more involved. To
motivate the correct definition, consider the following
argument.
In
Einstein's theory, the strength of the gravitational
coupling is the number Ǧ=G
k2, where G is
The
renormalization group will change this.
More
generally, in any field theory there will be in
principle infinitely many couplings [g]. If a
coupling g has
canonical mass dimension d we
define the dimensionless number ǧ = g k-d . The set of all these variables
parametrizes a space that we may call "theory space",
because it parametrizes all the possible actions.
Parametrizing theory space with the dimensionless
couplings [ǧ] just means that we are using the cutoff k as a
unit of mass. Naively all the ǧ whose corresponding g has
negative mass dimension would seem to diverge when k goes to
infinity. Instead, on a trajectory approaching a fixed
point, they would reach finite limits.
Q: Do we really have to consider all
possible couplings?
A: Actually, if a coupling can be eliminated
by a field redefinition it cannot enter into any
physical observable and therefore it need not have a
finite UV limit. Such couplings are called redundant or
inessential. By fixing a field parametrization one can
divide the set of all couplings into essential and
inessential, and in general there will be infinitely
many of each type. At a fixed point all the essential
couplings must have the behavior described above.
(Note also that it might happen that not all essential
couplings in our theory enter observables independently.
If, e.g. certain couplings enter observables in a
certain combination, only this combination has to show a
fixed point. Thus potentially the theory could yield
finite predictions even if some couplings would diverge
at a certain scale, but the combination in which they
enter observables stayed finite.)
Q: If it is desirable that the
renormalization group flow tends to a fixed point,
then the best theory should be one for which all points in
theory space are attracted towards it?
A: If all points in theory space were
attracted towards the fixed point, then we would have a
good UV limit irrespective of the initial conditions.
This would leave us with infinitely many arbitrary
couplings, each one of which would have to be determined
by experiment, and the theory would lose predictivity.
Instead,
we want to use the condition of having a good UV limit
as a way of selecting physically acceptable
trajectories. From this point of view the ideal case
would be that in which a single trajectory reached the
fixed point. This would pin down the theory uniquely.
More generally, if the FP has a finite number n of
attractive directions, then the set of trajectories that
are physically acceptable has dimension n-1. The
set of all points belonging to these trajectories is a n –
dimensional surface called the “UV-critical surface” or
the “unstable manifold”. In order to have a good UV
limit the initial point of the RG flow must lie in this
surface.
In an
asymptotically safe theory we would have to perform n
experiments at some given energy scale k to pin
down completely our position in theory space. Everything
else could then be computed, at least in principle, and
would constitute genuine predictions that could be
verified experimentally.
Q: How can we study the critical surface?
A: We can determine the tangent space to the
critical surface at the fixed point, by linearizing the
flow at the fixed point. The directions that are
attracted towards the fixed point in the ultraviolet are
called “relevant”. This is described more technically here (in .pdf format) (alternatively here in .ps
format) . This is enough to make predictions that
hold at high energies. As we move towards lower energies
the surface deviates from linearity and it gets very
hard to say much. (Note that this is true also in the
case of perturbatively renormalizable theories.)
Q: What does asymptotic safety correspond
to in perturbation theory?
A: Standard perturbation theory corresponds
to the case when the fixed point is the Gaussian (free
theory) fixed point. In this case the linearization of
the flow is described in technical terms here (in .pdf format) (alternatively here in .ps
format) . The tangent space to the critical
surface is spanned by the couplings that have positive
or vanishing mass dimension, i.e. those that are power
counting renormalizable (or marginal). Thus
asymptotic safety at the Gaussian fixed point is
equivalent to perturbative renormalizability plus
asymptotic freedom. It is widely agreed that a theory
with these properties makes sense up to arbitrarily high
energies and therefore can be regarded as a fundamental
theory. Asymptotic safety is a generalization of this
behaviour to the case when the fixed point is not a free
theory.
Q: If we cannot use perturbation theory
we cannot calculate anything so we may as well give
up.
A: There are important examples in nature
where physics simply becomes non-perturbative. This is
not a question of our choice or taste. As an example,
QCD at low energies exhibits non-perturbative phenomena
such as confinement and chiral symmetry, which are
accompanied by an explicit breakdown of perturbation
theory. There are non-perturbative methods such as
lattice gauge theory, Dyson-Schwinger equations and Functional
Renormalisation that can be used to gain understanding
of the non-perturbative regime.
It should also be said that if a nontrivial fixed point
is not too distant from the free one, in
some suitable sense, it may be possible to
study its properties using perturbation theory.
Q: Do we know any QFT that is
asymptotically safe?
A: QCD is asymptotically safe: it has a fixed
point (the free theory) and only finitely many couplings
are attracted towards it in the UV, namely the
Yang-Mills coupling and the quark masses. All other
couplings are repelled from it, so in order to have a
good UV limit one sets them to zero. (To be more
precise, one sets them to zero in perturbation theory.
i.e. in a neighborhood of the fixed point; further away
low orders in perturbation theory may be insufficient,
the critical surface may be curved and the relevant
couplings could contain some admixture of operators with
negative mass dimension).
Q. Do we know any QFT that is
asymptotically safe without being asymptotically free?
A: The Gross-Neveu model in two dimensions
with a p-2+ε
propagator, which is perturbatively nonrenormalizable,
has been rigorously shown to be renormalizable at a
nontrivial fixed point. See Gawedzki and Kupiainen
(1985a,b,c). A similar result in three dimensions has
been proven by de Calan et al (1991). For a more recent
discussion see Braun, Gies and Scherer (2010).
Q. Are there other examples of systems
that are governed by a nontrivial fixed point?
A:
A scalar field theory in three dimensions has a
nontrivial fixed point which gives a rather accurate
description of many critical phenomena. Of course in
this case one does not need to go to arbitrarily high
energies because condensed matter systems have a natural
cutoff at the atomic scale. However the existence of the
fixed point guarantees that there can exist systems
where the ratio between the overall size of the system
and the UV scale is arbitrarily large.
Q: What is the status of gravity in
perturbation theory?
A: If we restrict the action to contain only
the Hilbert term there is a “Gaussian” fixed point that
corresponds to vanishing
If we
enlarge the set of actions to include terms quadratic in
curvature then perturbation theory shows that no new
terms are generated by the quantum corrections, so the
theory is perturbatively renormalizable (Stelle 1977,
Voronov and Tyutin 1984). The reason why this is not
generally hailed as the quantum theory of gravity is
that actions quadratic in curvature generically
describe, in addition to the graviton, also other
massive spin two particles with the wrong sign in the
propagator (ghosts). It is not at all clear that the
presence of ghosts in the action near the fixed point is
fatal; some early comments in this sense can be found in
the papers of Julve and Tonin 1982, Salam and Strathdee.
But neither do we have a proof of unitarity, so the
point remains for the time being obscure.
Another
potential problem is that the proof of renormalizability
relies on flat space perturbation theory and hence
requires that the cosmological constant vanishes
identically. This seems to be inconsistent with the
Wilsonian flow.
Q: Why can one not neglect the
cosmological constant?
A: Essentially because the cosmological
constant runs too. We can fix our renormalization
conditions in such a way that it vanishes at some energy
scale but then it will be nonzero at other scales. A
more technical explanation can be found here (in .pdf format) (alternatively here in .ps format).
It shows that the flow in the neighbourhood of the
Gaussian fixed point must have the structure illustrated
in the following figure:
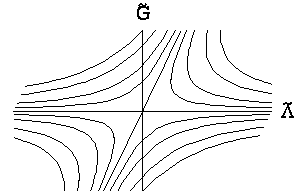
Fig.1: the flow in the perturbative region.
The point
here is the slant in the eigenvectors at the origin. If
both eigenvectors were directed along the axes, it would
be consistent to have nonzero
Possibly, a unimodular quantum theory could also become
asymptotically safe, in which case the cosmological
constant would not be a running coupling. This option is
so far unexplored.
Q: Where does the flow lead to?
A: According to all the calculations done up
to now, it leads to a nontrivial fixed point located
somewhere in the upper right quadrant, corresponding to
positive cosmological constant and
Note that neither the microscopic
cosmological constant nor the microscopic Newton
coupling need to be positive in order to be consistent
with observations: It suffices that they flow towards
the observed positive values at smaller momentum scales.
Since we know that higher-curvature operators also have
non-zero couplings at the fixed point, the positivity of
Newton's coupling is not required for the stability of
the theory. So far, we do however not know an example
where the flow crosses the line G=0, which suggests that
the fixed-point value of Newton's coupling should be
positive in order for the flow to be compatible with
observations in the infrared.
Q: To study the flow further from the
Gaussian fixed point we cannot use perturbation
theory. What can be used?
A: The most powerful instrument is the Exact
Renormalization Group Equation or ERGE. There are
different version of it; a popular one is the Polchinski
equation (Polchinski 1983). It is a functional equation
obeyed by the interaction part of the Wilsonian action.
For some applications it has proven more convenient to
use another equation for the Legendre transform or
effective average action Γk[Φ]
(Wetterich 1993, Morris 1994a,b).
The basic
idea behind these equations goes back to
An
important aspect of all this is the “cutoff” function
which is used to suppress the contribution of the low
momentum modes. This function is required to go quickly
to zero for momenta larger than k and to
some finite value for momenta going to zero. Aside from
this, the cutoff function is arbitrary. In general,
results obtained from the ERGE will depend on the choice
of this function. However, physical results must be
independent of the shape of the cutoff.
Q: I am not familiar with the ERGE. Does
it agree with the familiar results when perturbation
theory is applicable?
A: The ERGE gives the renormalization group
flow of the functional Γk[Φ] and
this functional contains in principle infinitely many
couplings. So the ERGE contains the beta functions of
all these couplings. It can be regarded as the “beta
functional” of the theory.
If the
average effective action Γk[Φ] is
written as a sum of generic operators On[Φ]
with coefficients gn
, then the coefficient of On[Φ]
in the
ERGE is the beta function of gn
. With some work one can extract the beta functions of
individual couplings from the ERGE. When applied to
scalar, fermion and gauge theories, this procedure can
be used to reproduce the results that are well known
from perturbation theory.
As
mentioned above, in general the beta functions depend on
the shape of the cutoff. This is similar to the
dependence on the renormalization scheme in perturbation
theory. However the leading terms in the beta functions
of dimensionless couplings (quartic scalar coupling,
Yukawa coupling, gauge coupling) turn out actually to be
independent of the shape of the cutoff (they are
“universal”) and agree with the results of perturbation
theory.
Q: The ERGE uses a cutoff. Does this not
conflict with gauge invariance?
A: There is a well established way of
quantizing gauge theories that preserves a form of gauge
invariance: the background field method. One can define
the ERGE for a gauge theory using the background field
gauge and using the background field in the definition
of the cutoff function. The average effective action is
then a functional of two fields Γk[Ā;A],
where Ā is
the background field and A is the
“classical” field introduced with the Legendre
transform. This functional is gauge invariant when both
arguments are gauge transformed. The background field is
arbitrary and at the end of the day one can set Ā=A. In this
way one obtains a gauge invariant functional of a single
gauge field, whose flow can be calculated using the
ERGE. As mentioned above, this reproduces the beta
function of the Yang-Mills coupling in the case of a
gauge theory. In the case of gravity this has been
discussed in Reuter 1998.
Q: How
do you define the scale k, when you want to integrate
over all possible metric configurations? The
definition of k requires the notion of a metric.
A: Here
the background field method is crucial: Picking a
background metric allows to define the notion of a scale
k, according to which we define metric
fluctuations to be "high energetic" or "low energetic"
modes. A priori, any metric is as good as any other.
However we should note that one distinguished metric
emerges dynamically: it is the solution of the quantum
equations of motion in the limit k-->0,
where all quantum fluctuations have been integrated out.
Q: What ultraviolet regularization do you
use?
A: There is no need to use any ultraviolet
regularization. The ERGE gives automatically finite
results for the beta functions because it receives
contributions only from field modes with momenta
comparable to k .
Technically
this is due to the fact that the k-derivative
of
the IR cutoff in the r.h.s. of the ERGE is a function
that tends to zero very rapidly when the momentum is
greater than k. This
effectively provides an UV cutoff for the trace in the
r.h.s. of the ERGE.
Yes, it is
somewhat confusing that an IR cutoff should work as an
UV cutoff, but this is one of the nice properties of the
ERGE.
Q: If k is an
infrared cutoff, how can it be used to study UV
physics?
A: It is an infrared cutoff in the sense that
in the definition of the generating functional it sets a
lower limit to the functional integration. It does not
mean that k has to
be small in any sense. Once the beta functions of all
couplings have been calculated, they can be used to
study the limit when k goes to
infinity.
Q: Still, the definition of the
functional Γk[Φ] requires some form of UV
regularization at scales Λ >> k
. So, you cannot study the limit when k goes to
infinity without having previously defined the limit
when Λ goes
to infinity.
A: Indeed, if we
wanted to define the functional Γk[Φ] from the
functional integral, then we would have to use some
ultraviolet cutoff Λ
>> k. But the derivative of Γk[Φ] with
respect to k does not
need any UV regulator, as I said before. So, we apply
the following logic:
1. We know that if the functional Γk[Φ] exists it
obeys the ERGE
2. We assume that a functional Γk[Φ] exists
3. We study the flow of Γk[Φ] using the
ERGE, which is well defined
4. If the flow has a FP with the desired properties, then the UV limit in k is well defined
Q: What does the ERGE say about the
running of
A: First of
all one must clarify that since the background field
effective action is a functional of two metrics (or
equivalently a metric and a fluctuation field), there
are actually two separate notions of Newton's constant.
Most of the work has been done on the coupling that
multiplies the background Einstein-Hilbert action, but
the available evidence suggests that the "other"
Newton's constant has a qualitatively similar behavior.
Starting from very low energies, where perturbation
theory is applicable, one finds a RG running of
Of course
the perturbative calculation cannot be trusted when Ǧ
becomes of order one. However, the ERGE is
not similarly limited. In fact with the ERGE one can
compute also all the higher powers of G0 in
the beta function. This leads to a finite shift in the
position of the fixed point, but qualitatively the beta
function is similar to the one loop result.
Q: Is there a heuristic understanding of
the gravitational antiscreening?
Q: If G(k) ≈ Ǧ k-2, could one not say that
A: To some extent this is a matter of
terminology, but I find that this statement would be
misleading.
Q: What does the ERGE predict for the
ultraviolet limit?
A: So far we have mentioned only
So far a
nontrivial fixed point has been found using each of the
following approximations to QGD:
1) The ε expansion of Einstein’s theory
around two dimensions
2) The leading order of the 1/N expansion
3) The Einstein-Hilbert truncation using a
variety of gauges and cutoff functions, also in the
presence of matter fields, both minimally and
non-minimally coupled.
4) A truncation including all terms with up
to four derivatives of the metric
5) A truncation involving polynomials up to
the eighth power in the Ricci scalar
6) The reduction of general relativity to
metrics admitting two Killing vectors
7) An infinite truncation with action of the form f (R).
8) Truncations involving a non-trivial gauge fixing
sector (bimetric truncations) and Faddeev-Popov ghost
sector.
9) A calculation using the Vilkovisky-DeWitt effective
action
Q: What does the ε expansion teach us?
A: This was historically the first hint that
there may be a nontrivial fixed point for
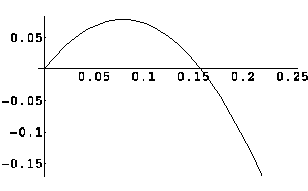
Fig.2: the beta function of
For further information on this
approximation see the series of papers by the Japanese
groups Kawai and Ninomiya 1990, Kawai et al 1993a,b,
1996, Aida et al 1994, 1997, Nishimura et al 1994.
Unfortunately it is not at all clear from
this procedure that the result can be trusted when ε is so large. One
reason is that dimensional regularization was used and
one may expect poles at rational values of the dimension
between 2 and 4. However, this result has been
subsequently vindicated by the ERGE, in the following
sense. In the ERGE there is no need for any ultraviolet
regulator so one can calculate the beta function in any
dimension d and follow the dependence of the results on
d without encountering any singularity. It turns out
that a fixed point exists for d>2 and the derivative
of the fixed point with respect to d, at d=2 is exactly
3/38. Furthermore, the number 3/38 is independent of the
shape of the cutoff function.
Q: What do you mean by a truncation?
A: Since we cannot in practice solve the ERGE
exactly, the most common approximation consists of
retaining just a finite number of terms in the
functional Γk[Φ]
and extracting their beta functions from the ERGE
without any further approximation. Such a procedure is
called a truncation. For example the Einstein-Hilbert
truncation consists in retaining only the cosmological
constant and
When we
truncate the action we neglect the effect that other
couplings can have on the running of the couplings that
are retained. There is no easy and direct estimate of
the errors that are being introduced in this way. One
indirect guess can be based on the scheme-dependence of
the results. We know that in the exact equation
“universal” quantities such as critical exponents must
be independent of the cutoff function. So the amount by
which they vary when the theory is truncated can be
taken as a measure of the quality of the truncation.
This kind of argument had been used by Reuter and
collaborators to argue that the results of the
Einstein-Hilbert truncation must be stable against the
addition of new couplings.
Of course
the best test is to calculate the effect of other
couplings on the results of the earlier truncation. For
the Einstein-Hilbert action, Codello Percacci and
Rahmede 2007 have checked that the addition of operators
up to eight powers in the Ricci scalar changes the fixed
point and the critical exponents only by few percent,
confirming the validity of the earlier conjectures.
Q: What do we learn from the
Einstein-Hilbert truncation?
A: The results of the Einstein-Hilbert
truncation are summarized in this flow diagram,
resulting from a numerical integration of the beta
functions:
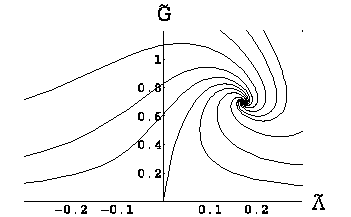
Fig.3: the flow of the dimensionless
cosmological constant and
It shows
the Gaussian fixed point in the origin, with the
behaviour anticipated in fig.1, and a nontrivial fixed
point at positive cosmological constant and
The
position of the fixed point depends on the cutoff
function. However it can be verified that the
dimensionless product of the cosmological constant and
Q: Does it make sense to have complex critical
exponents?
A: It
is only the real part of complex critical exponent that
decides about the relevance of a coupling. The imaginary
part signals that the flow approaches the fixed point in
a spiral-type shape. Although exotic, they are not
unknown in condensed-matter systems.
Whether some of the critical exponents remain complex
beyond the Einstein-Hilbert truncation is actually
unclear.
Q: What is known about curvature squared
terms?
A: The beta functions of higher derivative
gravity (including terms with four derivatives of the
metric) had been calculated earlier by several authors
using dimensional regularization (see Peixoto and
Shapiro 2006 for the state of the art of those
calculations). It had been found that the dimensionless
couplings (the inverses of the coefficients of the
four-derivative terms) are asymptotically free. However,
the status of the cosmological constant and
These
calculations have been repeated using the ERGE by
Codello and Percacci (2006). Technical complications
have further required the use of the one loop
approximation and an expansion in powers of the
cosmological constant. The beta functions of previous
authors have been exactly reproduced, but some
additional terms appeared in the beta functions of the
cosmological constant and
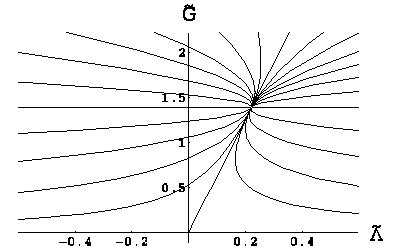
Fig.4: the flow of the dimensionless
cosmological constant and
It is
therefore found that the ERGE reproduces the universal
beta functions of dimensionless couplings as computed in
perturbative approaches. On the other hand the ERGE is
uniquely suited to discuss the behaviour of the
dimensionful couplings, which appear to reach a
nontrivial fixed point.
More
recently Benedetti et al (2009) have calculated these
beta functions without some of the approximations made
before. In a four parameter truncation (the flow of the
topological term is not calculated) the critical surface
appears to be three dimensional. As expected, all
couplings tend to finite nonzero limits. This behavior
persists also in the presence of a scalar field.
Q: What can be said about higher powers
of curvature ?
A: So far only higher powers of the curvature
scalar have been studied. Codello et al (2007) and
Machado and Saueressig (2007) have studied Lagrangians
of the type f(R), with f a polynomial of order up to six
(later extended to eight), and shown that a fixed point
exists and has a three dimensional critical surface.
The flow equation can be written for the whole function
f but initially it proved too hard to solve. A
simplified form of the flow has been later proposed by
Benedetti and Caravelli (2012) and fixed point solutions
have been found by Dietz and Morris (2012). This is a
very powerful extension of previous truncations because
it shows that the fixed point exists even when one
considers an infinite number of couplings. This has the
same level of sophistication of studies of scalar
theories in the "local potential approximation", where
one allows the potential to be completely general.
Q: Quite impressive, but is it good
enough? We need a fixed point for all possible
couplings. How can you think of ever proving its
existence ?
A: This looks hard indeed. But there exists at
least some approximation where one can prove the
existence of the fixed point for all couplings: it is
the leading order of the 1/N
approximation.
In a
gravitational context N is the
number of matter fields coupled to the metric. Each one
of these matter fields gives a contribution to the
gravitational effective action and hence to the
gravitational beta functions. If the number of such
fields goes to infinity the contribution of graviton
loops can be neglected relative to that of matter loops.
Notice that this may actually be a reasonably good
approximation in the real world, where there is only one
graviton and dozens of matter fields (in GUTs there may
even be hundreds of matter fields).
Tomboulis
1978, 1980 has shown how to turn this into a systematic
expansion. Here we are only interested in the leading
order of this expansion, which consists in neglecting
the graviton contribution altogether. This simplifies
calculations dramatically: the beta functions are just
constants. This allows one to establish the existence of
the fixed point at all orders in the derivative
expansion of the gravitational action.
For a
generic cutoff function one finds that all the couplings
have nonzero values at the fixed point, with the
exception of the dimensionless ones (the coefficients of
the curvature squared terms) which tend logarithmically
to infinity (equivalently, their inverses are
asymptotically free); the critical exponents are equal
to the canonical dimensions, so the dimension of the
critical surface is five. There is a special class of
cutoff functions such that the coefficients of Rn
with n>2 all vanish. (This is related to a
remark made by Chamseddine and Connes (
This gives
us a mechanism that can be easily understood and
generates a fixed point for the whole infinite set of
couplings of the derivative expansion.
Q: What does the two-Killing vector
reduction teach us?
A: In this reduction one keeps the most
general form for the gravitational action but cuts the
number of degrees of freedom by imposing the existence
of two Killing vectors. In this case gravity becomes a
specific sigma model which has been shown by Niedermaier
2002, 2003 to be asymptotically safe.
Q: What do we know about the critical
surface beyond linearization?
A: In the Einstein-Hilbert truncation there is
a critical trajectory that flows from the nontrivial
fixed point to the Gaussian fixed point, as energies are
lowered. See Fig. 3. This critical trajectory obviously
lies in the critical surface. It can be studied
numerically and is there for all choices of gauge and
cutoff. It is is also there at one loop in the presence
of curvature squared terms, see fig.4 , but it is not
known whether it exists also with higher truncations
(some results on this issue in the R^2 truncation have
been given by Rechenberger and Saueressig (2012)).
Q: What is the behavior of the graviton
at high energy in asymptotically safe gravity?
A: In linearized Einstein theory, the wave
function renormalization constant of the graviton is Z = 1/(16 π G)
. The anomalous dimension of the graviton is therefore η = -β/G,
where β is the
beta function of G. Since
at a gravitational fixed point β=(2-d) G ,
where d is the spacetime dimension, we conclude that at
a fixed point η = d-2 .
It means that the graviton propagator in the UV limit
behaves like p-2-η=p-d
. Such a large, integer anomalous dimension appears also
in other gauge theories away from the critical
dimension, see e.g. Gies (2003) or Kazakov (2003).
Q: If gravity is asymptotically safe,
what does spacetime look like at short distances?
A: One general conclusion that can be drawn is
that spacetime geometry cannot be understood in terms of
a single metric: rather, one should use a different
effective metric at each momentum scale. This had been
suggested by Floreanini and Percacci 1995a,b, who
calculated the scale dependence of the metric using an
effective potential for the conformal factor. Such a
potential will be present in the effective action Γk[Φ] before
the background metric is identified with the classical
metric (as mentioned in section 1.2). In the context of
the ERGE, Lauscher and Reuter 2005 have discussed a
running metric emerging as a solution of a running
average effective action in the Einstein-Hilbert
truncation.
A set of
metrics depending on the scale can be seen as a
description of the fractal geometry of spacetime. Quite
generally, from dimensional analysis it follows that the
effective metric must run as k-2
(here we assume the coordinates to be dimensionless).
This affects the propagation of other fields. A
phenomenon characterized by an energy scale k will
“see” the effective metric at scale k . For a
(generally off-shell) free particle with four--momentum
p (as
measured by some fiducial metric) it is natural to use k = p .
Its inverse propagator will then behave at high energy
as p-4
, independent of spacetime dimension. In four dimensions
this agrees with the result derived above for the
propagator of graviton. That these two arguments should
give the same result only in four dimensions is quite
intriguing.
Note that the anomalous dimension for matter fields
typically is not -2, so this would suggest that matter
propagators do actually not show a scaling that leads to
a logarithmic real space propagator as in 2 d.
It is also important to realize that there are many
different notions of dimensionality, and what we usually
think of as dimension is indeed the topological one.
This does not show any change in asymptotic safety from
IR to UV and is always 4. What does show a
scale-dependence is the spectral dimension. This
definition of the dimension relies on the properties of
a fictitious particle probing the Euclidean space-time
in a random walk without any back reaction. This
dimension shows a scale dependence and runs towards 2 in
the ultraviolet. This result is shared by several other
approaches to quantum gravity, but it is important to
realize that it does not mean, that space-time becomes
two-dimensional in a naive way, i.e. quantum gravity in
the UV is not simply described by some theory with
topological dimension 2 (i.e. \int d^2 x).
Q: Can we test this fractal structure in
some way?
A: We cannot currently test it in the lab but
we can do so in numerical simulations. Ambjřrn,
Jurkiewicz and Loll 2005a,b have studied the propagation
of a scalar particle in a dynamically triangulated
spacetime, with a discretized version of the Einstein
dynamics. They have found that for short time scales the
spectral dimension of the triangulated spacetime is two,
while for long time scales it tends to four. This could
be related to the result mentioned above by observing
that a propagator that decays like p-4 in Fourier
space decays logarithmically in coordinate space, and
this is the typical behaviour of propagators in two
dimensions.
Q: I believe that spacetime must be
discrete at short distances.
A: Before
answering the question whether spacetime is discrete or
continuous, one has to specify how lengths are going to
be measured. In general, units of length can be traced
to some combination of the couplings appearing in the
action. For example, in Planck units one takes the
square root of
Recent work of Bianca Dittrich supports
this conclusion from another perspective. It is possible
to define discrete theories where the dynamics
correspond exactly to the dynamics of a continuum
theory. The question whether space-time is discrete or
continuous may therefore very well be only a matter of
description, and not a physical distinction.
Q: If gravity is asymptotically safe,
almost certainly it will contain higher derivative
terms. Is this not going to spoil unitary?
A:
A theory that contains R^2-type operators (we disregard
the tensor structure here), is non-unitary around a flat
background in perturbation theory. There are several
ways in which this conclusion could be avoided:
- The couplings in the propagator are running couplings:
Depending on how they actually run, the ghost pole of
the propagator could actually never be reached (see
Floreanini and Percacci (1995), Benedetti, Machado,
Saueressig (2009)).
- The fixed-point action will presumably contain
infinitely many non-zero couplings, thus it will not be
a simple polynomial in R. The question of ghost poles
then boils down to the question where the full
propagator has poles. It may well be that a finite
truncation of the effective action shows fictitious
poles in the propagator, that are not present in the
full propagator.
- The flat background is probably not a solution of the
effective equations of motion. The question of unitarity
requires us to first find the correct vacuum, and then
look at the second order in fluctuations around this
background.
So the
answer is that we do not know. Available information on
the FP action is certainly not enough to decide.
Q: OK, let’s assume that all this is
true. How do we relate it to the low energy world that
we are familiar with?
A: The fixed point action describes the world
at Planckian scales and beyond. In order to relate it to
known phenomenology we should evolve the renormalization
group flow down to the energy scales of particle
physics. Reuter and Weyer (2004) have discussed this in
the context of the Einstein-Hilbert truncation. They
show that the existence of an extended semiclassical
regime, where the dimensionful cosmological constant and
Newton’s constant are essentially constant, implies that
the world must lie on a trajectory that is very close to
the critical trajectory of fig.1 and then turns toward
the right (when going towards the infrared).
The
leftmost point on this trajectory, which is called the
turning point, must correspond to an energy scale of the
order of the milli-eV. The trajectory then apparently
hits an infrared singularity when the dimensionless
cosmological constant becomes equal to ˝. This happens
at energies of order of the Hubble scale. The infrared
singularity could be an indication that the
Einstein-Hilbert truncation becomes insufficient at
these scales. More recently there have been hints that
there is an IR fixed point there.
Q: Can there be observable consequences
for high energy physics?
A: As usual
with quantum gravity, strong observable effects will
only manifest themselves at the Planck scale. If the
world is four dimensional there is at present little
hope of observing directly the consequences of the
asymptotically safe behaviour in the laboratory.
However, in theories with higher dimensions the Planck
scale could be at the TeV scale. Then, signals of
asymptotic safety could be observed at colliders. Hewett
and Rizzo 2007, Litim 2007, Koch 2007 have discussed
several processes including graviton-mediated Drell-Yan
processes, graviton production and black hole production
at LHC, both for large extra dimensions and warped extra
dimensions scenarios. They find improvements in the high
energy behaviour of the cross sections due to asymptotic
safety, which provide distinctive signatures for this
scenario.
At lower
scales and in four dimensions, the effects are
suppressed by powers of the energy scale over the Planck
scale. Thus another way to access quantum gravity is to
reach a very high experimental precision and/or to
concentrate on processes that would be otherwise
forbidden, or processes that could accumulate over large
distances, as with the propagation of light from distant
sources.
In connection with these scaling relations, it is
important to realise that canonical power counting does
not hold at a non-Gaussian fixed point. Operators that
by canonical power counting would be suppressed by some
power of the Planck scale could indeed show a large
anomalous dimension that would make them less suppressed
than we think naively.
Another way to indirectly test asymptotic safety would
arise if the existence of the fixed point required
certain properties of the matter sector, such as
limitations of the number and types of allowed fields.
Q: Can there be observable consequences
for astrophysics?
A: An application of the running
Q: Can there be observable consequences
for cosmology?
A: Several authors have tried to use the
renormalization group running of gravitational couplings
in a cosmological context. However not all these
attempts are necessarily related to asymptotic safety.
In some cases beta functions have been postulated that
have no relation to those calculated from the ERGE.
The
starting point is always to link the renormalization
scale k to some
cosmological parameter. The most popular choice seems to
be the Hubble scale, which is related to the curvature
of the universe at large scales. Then, the running
Since
asymptotic safety is concerned with the ultraviolet
behaviour of the theory, its impact in cosmology will
probably be most important at the very earliest stages
of cosmic history, e.g. the inflationary era. In fact,
it has been shown that asymptotic safety could generate
inflation with approximately 60 e-foldings and an
automatic exit without the introduction of an extra
scalar field and a highly fine-tuned potential (Bonanno,
2012). Furthermore,
the cosmological constant runs down to arbitrarily low
energy scales and this has been linked by Bonanno and
Reuter (2007) to the generation of the cosmic entropy.
Q: What
is the relation of asymptotic safety to other
approaches to quantum gravity?
A: This is a question that cannot be answered
definitely at the moment. The most promising
similarities are with Causal Dynamical Triangulations,
which shares the same general ideology and exhibits
similar behavior of the spectral dimension.
Also there exist approaches such as group field theory
that postulate that at the fundamental level,
gravitational degrees of freedom are fields on an
abstract group manifold. Spacetime emerges effectively
when the theory goes through a second-order phase
transition. A point of contact to asymptotic safety
would arise, if this second-order phase transition could
be related to the fixed point seen in the RG flow, and
the critical exponents of the second-order phase
transition were those that have been found for the fixed
point in the RG flow.
Some
similarities between the functional RG flow for gravity
and the holographic RG flow have been pointed out in
Litim, Percacci and Rachwal (2010). The relation between
asymptotic safety and the notion of "classicalization"
has been discussed to some extent by Percacci and
Rachwal (2011).
Q: Has the functional RG, on which most results about
asymptotic safety in gravity rely, been tested for
other theories?
A: The functional RG has been tested extensively
in other physical models, ranging from QCD in the
non-perturbative regime over scalar O(N) theories to
phase transitions in ultracold quantum gases.
In all of these examples, other methods and experimental
results exist to which the results from the FRG can be
compared, and these comparisons show that the FRG is a
reliable method. As with all methods in the
non-perturbative regime, it is highly non-trivial to
control the systematic error of the truncation, but in
principle, the results from the FRG can be extremely
accurate, as the example of critical exponents in scalar
O(N) theories demonstrates.
Q: Is it possible to have more exotic UV completions?
A: In
principle, the physical requirement is that observables
stay finite for all finite values of the RG scale k.
This could also be accomplished by a limit cycle (see
Litim, Satz (2012) and Bonanno, Guarnieri (2012)), or
some more complicated attractor in theory space.
Furthermore, even a trajectory on which the couplings
stay finite at all finite momentum scales and only
diverge at k -> \infty provides for a UV complete
theory (an example of a toy model that admits such a
trajectory in a simple truncation is axion
electrodynamics (Eichhorn, Gies, Roscher (2012))).
Q: Can asymptotic safety solve the triviality problem
of the Standard Model?
A: The
triviality problem occurs in QED as well as scalar Φ4 theory in
four dimensions (thus presumably affecting the Higgs
sector of the standard model). The fact that the running
coupling hits a Landau pole at a finite RG scale implies
that if the cutoff of the theory is to be taken to
infinity (thus making it a fundamental as opposed to an
effective theory), the IR value of the coupling will be
zero. Thus the theory requires a more complicated UV
completion with further degrees of freedom.
In principle, the Landau pole could be removed due to
the effect of quantum gravity fluctuations and the RG
flow of, e.g. gravity+QED could approach a common fixed
point in the UV, thus solving the triviality problem.
Q: Can asymptotic safety help to reduce the number of
free parameters of the standard model?
A: At
a non-Gaussian fixed point, canonical power-counting
arguments break down. Thus the relevance of a coupling
is not determined by its canonical dimensionality alone,
but depends on the effect of quantum fluctuations. Thus
operators that we classify as relevant in perturbation
theory (such as the gauge couplings and masses in the
standard model), could in principle become irrelevant at
a non-Gaussian fixed point for the
standard-model+gravity system. Then some of the free
parameters of the standard model could be predicted. An
intriguing example that this might be the case has been
found in Reuter, Harst (2011), where a U(1) gauge theory
coupled to gravity admits a non-Gaussian fixed point
where the gauge coupling becomes irrelevant. In
principle, this could lead to a prediction of the fine
structure constant.
Q: Is there an infrared fixed point? What does this
have to do with asymptotic safety?
A: A
number of papers have recently found hints of a possible
infrared fixed point (Nagy, Kriszan, Sailer (2012),
Rechenberger, Saueressig (2012), Litim, Nicolai,
Pawlowski, Rodigast (2012)). These results were based on
the same functional RG methods that are used to study
asymptotic safety, but but if this infrared fixed point
exists, then it is independent of the UV completion for
gravity.
Q: How many degrees of freedom are there in
asymptotically safe quantum gravity?
A: Within
the asymptotic-safety scenario the degrees of freedom
are not fixed a priori. They are only constrained in
that we insist that they should be carried by certain
fields (the metric, but possibly a tetrad and possibly
even an independent connection). In fact, the degrees of
freedom then depend on the operators in the fixed-point
action. In principle, further, lower spin degrees of
freedom could become dynamical in addition to the
massless spin-2 mode of Einstein gravity.
Q: Could we also use a first-order formulation in
terms of vielbeins? Could torsion be dynamical in
asymptotic safety?
A: Asymptotic
safety is a proposal for a UV completion of any quantum
field theory, and a priori comes with no requirements
about the fields that carry the degrees of freedom. Thus
the standard metric theory space as well as a theory
space using vielbeins as the carriers for the
gravitational degrees of freedom could admit a
non-Gaussian fixed point.
First explorations of vielbein theory spaces with
dynamical torsion have been carried out by Daum and
Reuter (2011), where the RG flow of the Newton coupling,
cosmological constant and the Immirzi parameter was
studied and a non-trivial fixed point was found. The
analogue of the Einstein-Hilbert truncation in a
vielbein theory space was investigated in Harst and
Reuter (2012) and Dona', Percacci (2012). They found a
non-trivial fixed point for the Newton coupling and the
cosmological constant, however with a more severe
scheme-dependence than in the metric theory space.